|
PPXX バルク or
導波路
Figure shows “input
wave”, converted output, material's nonlinearity χ(2)
|
|
The
interaction between electro-magnetic field and dielectric
material results in an induced polarization field within the
material. Normally, the response of the material is linear, as
shown in figure below. In the nonlinear medium, polarization
vector is not proportional to optical electric field and can
be expressed as Taylor series expansion:
|
|
|
| where Pi
is the ith component of polarization vector. Ei is
the ith component of input electric field. χij(1)
is linear susceptibility, while χijk(2)
and χijkl(3) are the second-order and
third-order nonlinear susceptibility. In other words, the
susceptibility can be expressed as |
|
|
|
The
linear term χ(1) determines the linear propagation
of optical waves (including refraction, reflection,
diffraction and dispersion.), while the higher order terms
(such as χ(2) and
χ(3)) correspond to nonlinear effects under strong
electrical fields. The second order term χ(2)
vanishes in materials with inversion symmetry structures but
could be large in several nonlinear materials such as Lithium
Niobate (LiNbO3).
<![endif]>
In nonlinear materials with χ(2), a light with
frequency ω will generate a nonlinear polarization vector:
|
|
|
| where dijk(=χijk(2))
is the nonlinear coefficient. This polarization vector will
induce a double-frequency electric field. Such process is
called χ(2) frequency conversion or mixing
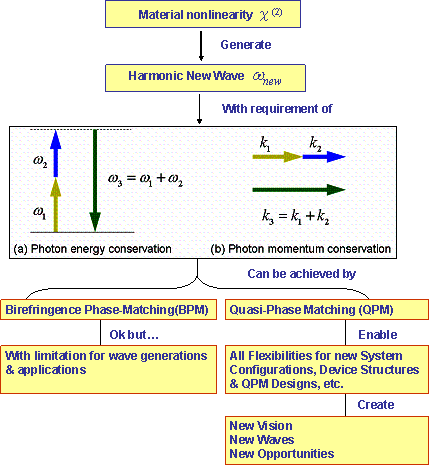
process. To enable efficient conversion, both the photon
energy conservation and photon momentum conservation are to be
achieved simultaneously, as shown in figure below. The
requirement on the photon momentum conservation is also called
“phase-matching” constraint. |
|
|
Birefringence-Phase-Matching (BPM) |
|
In order to achieve efficient wavelength conversion, phase
matching between interaction waves are required.
Traditionally, this has been done in nonlinear materials
through birefringence phase matching techniques, which orient
crystal axis to a specific angle to achieve phase matching
condition for specific interaction wavelengths. However, such
techniques can not enable efficient use of material's full
transparency wavelength ranges at optimized conversion
efficiency. In addition, Birefringence phase-matched frequency
conversion processes occur in the presence of both ordinary
and extraordinary polarized radiations. While propagating
along non-optic axis direction of a NLO crystal, the
extraordinary waves suffer birefringence walk-off; whereas
ordinary rays do not. Thus this walk-off issue (the converted
wave diverges from the fundamental wave) will limit the
effective interaction length and distort the beam quality, and
hence limits the conversion efficiency of birefringence
phase-matched NLO processes.
Take SHG as an example, the refractive index of the
fundamental wave must be equal to that of SHG wave to achieve
birefringence phase matching under specific wavelength
condition. Therefore, the fundamental wave will be oblique an
angle θ to the optical axis (c-axis) of the nonlinear optical
crystal.
|
|
|
Quasi-Phase-Matching (QPM) |
|
Quasi-phase matching is a technique for
phase matching nonlinear optical interactions in which the
relative phase is corrected at regular intervals using a
structural periodicity built into the nonlinear medium. The
phase velocity difference is compensated by shifting the phase
relative to one another over a coherent distance through
inverting the sign of the nonlinear coefficient. And
therefore, the unidirectional power flow can be produced for
any mixing interaction for which the material is transparent.
The principle and effects of quasi-phase matching on nonlinear
frequency conversion are illustrated in the following figure.
It shows the phase matching condition for a quasi-phase
matching scheme, where the wave vector associated with a
periodic modulation of the properties of the nonlinear medium
compensates for the wavevector mismatch of the interacting
waves. The figure also shows the effect of quasi-phase
matching on second-harmonic generation using periodically
reversed domains as an example. In
the nonlinear medium, the distance over which the accumulated
phase difference of the interacted waves reaches π
is the "coherence length" lc. Without
phase matching, the generated second harmonic grows and decays
as the fundamental and second harmonic waves go in and out of
phase over each coherence length lc. In the
perfectly phase-matched case (as is obtained using
birefringence phase matching), the generated power grows
quadratically with crystal length. The
QPM method involves reversal of the sign of the nonlinear
coefficient at each
multiple of lc, also results in a net quadratic
increase with crystal length, where the discrete nature of the
reversals results in a lower second derivative than that
obtained with perfect phase matching. Instead of perfect
phase-matching everywhere like in the phase-matched case,
phase mismatch is discretely compensated in QPM gratings.
|
|
|
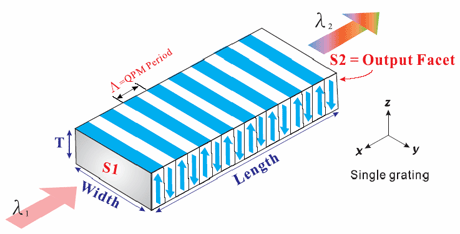
QPM structures are most commonly obtained by periodic poling
of ferroelectric crystals like lithium niobate (LiNbO3) and
lithium tantalate (LiTaO3). The most widely used method for
periodic poling makes use of electric fields. The principle is
that the spontaneous polarization in a ferroelectric material
such as lithium niobate can be reversed periodically under the
influence of a sufficiently large electric field (In general,
it is meant to be “periodically poled”). Such periodically
domain-inverted structures are used to compensate the phase
velocity mismatching between interaction waves based on QPM
techniques. Thus, the periodically poled devices are
engineered to maintain proper phase relationship between the
propagating waves, so as to maximize the efficiency of
non-linear frequency conversion. |
|
|
|
|
|
Note:
The comparisons are under the wavelength 1064nm
Reference: Data from the software “SNLO”
|
|
MgO:LN and MgO:SLT have been regarded as the attractive
nonlinear materials for the QPM devices because of their large
nonlinear coefficient, short-wavelength transparency, and high
resistance to photorefractive damage. They have attracted much
attention for use in high-density optical storage, and in
biomedical applications, because of its shorter wavelength and
higher photon energy. Recent development of higher-power
infrared and visible-red laser diodes makes it more realistic
to achieve compact UV source based on QPM MgO:SLT chip.
|
Convert or Amplify Pump Laser by Using
Specific Frequency Mixing Configuration
|
| As a difference from birefringence
phase matching, QPM technique utilizes full transparency
ranges (350 nm ~ 5000 nm in the case of lithium niobate) of
the non-linear materials and their highest non-linear
coefficient to achieve efficient optical frequency conversion.
This enables efficient wavelength conversions via different
wave-mixing schemes. Examples of frequency mixing
configurations are illustrated below: |
|
|
|
Frequency Mixing Configuration
|
Choose PPXX Bulk or Waveguide ? |
While PPXX bulk device
offers advantages of higher power and larger apertures
applications, PPXX waveguides (WG) can be used to further
enhance nonlinear efficiency mixing as compared to PPXX bulk
devices, by tightly confining the laser over long distances.
The tightly focused optical wave will often diffract when it
propagates in a bulk device, so single-pass high conversion
efficiency cannot be achieved. In waveguides, the mode profile
is confined to a transverse dimension in the order of the
wavelength, and hence high optical intensities can be
maintained over considerable distance to improve the
conversion efficiency by two to three orders of magnitude as
compared to bulk devices. Also, the nonlinear mixing
efficiency is quadratically proportional to the interaction
length of the waveguide device (linear proportional for bulk
devices), thus the fabrication of long, uniform and low-loss
waveguide is essential for highly efficient optical frequency
mixer. |
|
|
|
Bulk
and WG Frequency Conversion
|
Different QPM Patterns Allow Diverse Applications |
Other advantages of PPXX technology are its domain structures
defined by the mask patterning process, which provides
additional application dimensions unavailable by traditional
nonlinear bulk materials. Several others specific periodic
pattern designs such as cascaded, fan-out, and customized
configuration are also available for specific applications
using the CW, pulsed and ultra-short pulsed laser pumps. |
|
|
|
Various QPM Patterns
|